Contact - Liens - Plan du site - Bons plans Thomann - Conditions d’utilisation

HP et caisson de grave Part 2:

Un excellent article sur les caissons de basse, en 6 parties, paru dans le magazine sono, N°323 à 328, par Alain Pouillon-Guibert, Monsieur APG himself.

Les caissons de grave

Nous avons établi dans nos deux précédents numéros la justification de l'utilité de sources acoustiques dédiées aux fréquences graves. Les principes de base et les limitations physiques étant déterminées, passons aux applications pratiques.

COMMENT GÉNÉRER DU GRAVE?

Le ressenti physique des fréquences graves n'est pas le même que celui des fréquences médium et aigues. Si une forte pression dans l'aigu fait vriller vos oreilles, une forte pression dans le grave fait vibrer vos pantalons. Pourquoi ? Tout simplement parce que plus les fréquences générées sont basses, plus il faut "bouger de l'air*. Ce phénomène est visible sur les toiles ou les mousses qui recouvrent les faces avant de vos enceintes. Le mouvement de l'air à la sortie des évents provoque souvent une accumulation de poussiè­re localisée précisément à l'endroit où se trouvent les évents. En mettant sim­plement la main devant un évent de bass-reflex. vous pouvez ressentir le courant d'air.

Si maintenant vous déplacez la main devant la trompe d'aigu, vous ne res­sentirez rien du tout. A pression sono­re identique, l'aigu ne nécessite que très peu de déplacement d'air alors que le grave en a besoin de beaucoup plus. Je vous épargne quelques fastidieux calculs, mais permettez-moi de vous donner une seule formule qui va éclai­rer votre lanterne.

Si l'on considère qu'une source sono­re est une sphère puissante dont le dia­mètre est petit comparé aux longueurs d'onde générées, on peut calculer la pression sonore en fonction du volume d'air déplacé V (en m3), de la fréquence F (en Hz) et de la distance à laquelle on se trouve D (en m). SPL DB = 102.4 + 20 log(V) + 40 log(F) - 20 log(D).

Exemple 1 : Quel doit être le volume d'air déplacé pour obtenir 110 dB SPL à 1 m à 100 Hz?

110 = 102,4 + 20 log(V) + 80. Car 40 Iog100 - 20 log1 = (40 x 2) - 0 = 80.

Ce qui donne :

log(V) = (110-102.4-80)/20 soit V = 10 -3.62 ; V = 2.4.10-4 m3 soit 240 cm3.

Quelle est ta valeur du déplacement (X) de la membrane pour un HP de 30 cm. soit environ 26 cm de diamètre de rayon­nement (1) ?

V = SxX ; S = Pi x D2/4 soit 531 cm2; X = 240 cm3 / 531 cm3 = 0.45 cm. soit 4,5 mm.

Exemple 2: Quelle doit être l'augmenta­tion de volume d'air déplacé pour obte­nir le même niveau SPL en divisant la fré­quence par deux ?

Lorsque F est divisée par deux, V doit être multiplié par 4 (voir formule).

Pour générer 110 dB à 50 Hz. la mem­brane de notre HP de 30 cm devra donc se déplacer de 4.5 mm x 4 = 18 mm. Valeur largement supérieure à ce que peut admettre un HP stan­dard.

Exemple 3: Quelle doit être l'aug­mentation de volume d'air dépla­cé pour obtenir 10 dB de plus à la même fréquence ?

20 log (V2/V1) = 10 ; log (V2/V1) = 0.5 ; V2/V1 = 103,5 = 3.16.

Pour générer 120 dB (toujours à 1 m) à 100 Hz, la membrane de notre HP de 30 cm devra donc se déplacer de 4.5 mm x 3.16 = 14 mm Là encore, cette valeur est large­ment supérieure aux capacités mécaniques d'un HP standard. Seuls quelques HP spéciaux de *car audio* atteignent de tels dépla­cements. mais au prix d'une perte de rendement importante. Vous le saviez déjà : pour faire du grave, il faut de la surface et du déplacement, mais quelques exemples concrets permettent de clarifier et aussi de quantifier le problème. Les constructeurs de caissons de grave vont donc cher­cher à développer, ou simplement acheter des HP spécialisés qui répondent à la quadrature du cercle maximum de pression, minimum de volume de caisse.

COMMENT GÉNÉRER DU GRAVE?Le ressenti physique des fréquences graves n'est pas le même que celui des fréquences médium et aigues. Si une forte pression dans l'aigu fait vriller vos oreilles, une forte pression dans le grave fait vibrer vos pantalons. Pourquoi ? Tout simplement parce que plus les fréquences générées sont basses, plus il faut "bouger de l'air*. Ce phénomène est visible sur les toiles ou les mousses qui recouvrent les faces avant de vos enceintes. Le mouvement de l'air à la sortie des évents provoque souvent une accumulation de poussiè­re localisée précisément à l'endroit où se trouvent les évents. En mettant sim­plement la main devant un évent de bass-reflex. vous pouvez ressentir le courant d'air.

Si maintenant vous déplacez la main devant la trompe d'aigu, vous ne res­sentirez rien du tout. A pression sono­re identique, l'aigu ne nécessite que très peu de déplacement d'air alors que le grave en a besoin de beaucoup plus. Je vous épargne quelques fastidieux calculs, mais permettez-moi de vous donner une seule formule qui va éclai­rer votre lanterne.

Si l'on considère qu'une source sono­re est une sphère puissante dont le dia­mètre est petit comparé aux longueurs d'onde générées, on peut calculer la pression sonore en fonction du volume d'air déplacé V (en m3), de la fréquence F (en Hz) et de la distance à laquelle on se trouve D (en m). SPL DB = 102.4 + 20 log(V) + 40 log(F) - 20 log(D).

Exemple 1 : Quel doit être le volume d'air déplacé pour obtenir 110 dB SPL à 1 m à 100 Hz?

110 = 102,4 + 20 log(V) + 80. Car 40 Iog100 - 20 log1 = (40 x 2) - 0 = 80.

Ce qui donne :

log(V) = (110-102.4-80)/20 soit V = 10 -3.62 ; V = 2.4.10-4 m3 soit 240 cm3.

Quelle est ta valeur du déplacement (X) de la membrane pour un HP de 30 cm. soit environ 26 cm de diamètre de rayon­nement (1) ?

V = SxX ; S = Pi x D2/4 soit 531 cm2; X = 240 cm3 / 531 cm3 = 0.45 cm. soit 4,5 mm.

Exemple 2: Quelle doit être l'augmenta­tion de volume d'air déplacé pour obte­nir le même niveau SPL en divisant la fré­quence par deux ?

Lorsque F est divisée par deux, V doit être multiplié par 4 (voir formule).

Pour générer 110 dB à 50 Hz. la mem­brane de notre HP de 30 cm devra donc se déplacer de 4.5 mm x 4 = 18 mm. Valeur largement supérieure à ce que peut admettre un HP stan­dard.

Exemple 3: Quelle doit être l'aug­mentation de volume d'air dépla­cé pour obtenir 10 dB de plus à la même fréquence ?

20 log (V2/V1) = 10 ; log (V2/V1) = 0.5 ; V2/V1 = 103,5 = 3.16.

Pour générer 120 dB (toujours à 1 m) à 100 Hz, la membrane de notre HP de 30 cm devra donc se déplacer de 4.5 mm x 3.16 = 14 mm Là encore, cette valeur est large­ment supérieure aux capacités mécaniques d'un HP standard. Seuls quelques HP spéciaux de *car audio* atteignent de tels dépla­cements. mais au prix d'une perte de rendement importante. Vous le saviez déjà : pour faire du grave, il faut de la surface et du déplacement, mais quelques exemples concrets permettent de clarifier et aussi de quantifier le problème. Les constructeurs de caissons de grave vont donc cher­cher à développer, ou simplement acheter des HP spécialisés qui répondent à la quadrature du cercle maximum de pression, minimum de volume de caisse.

MAIS QU'EST-CE DONC QUE LA COMPRESSION THERMIQUE?

Le fil utilisé dans la fabrication des bobines mobiles est dans 99 % des cas, soit en cuivre, soit en aluminium. L'aluminium étant plus léger que le cuivre, il permet de faire des bobines plus légères aussi, sachant que la masse de la bobine est principalement constituée par la masse du fil. Chaque matériau est caractérisé par sa *résistivité* ρ (rδ) en Ω.m, inverse de la conductivité. qui permet de calculer la résistance globale d'un morceau de fil. La résistance d'un fil est donnée par la formule suivante : R = ρ x L/S. R étant exprimé en ohms (Ω). L. la longueur du fil. en m et S. sa section, en m3.

Le mouvement aléatoire des électrons dans le conducteur augmentant avec la température, ρ n'est pas constante et augmente aussi avec la température. Le courant électrique aura donc de plus en plus de difficultés à traverser le matériau, la résistance du matériau augmente.

Qu'en est-il de la force motrice ? Reprenons la formule de Laplace qui nous dit : F = B x I x L. La loi d'Ohm nous permet d'exprimer I en fonction de la tension aux bornes de la bobine : I = U / Z, Z étant l'impédance du HP qui comporte une partie purement résistive, R, la résistance de la bobine au courant continu, et Lω, partie selfique (réactive) dont la valeur augmente avec la fréquence (ω = 2 x Pi x F).

Seule R varie avec la température, je simplifierai donc l'explication en considérant que dans les basses fréquences. Z = R. Cette approximation est sensiblement valable pour des fréquences supérieures à la fréquence de résonance du HP et jusqu'à une centaine de Hz. c'est-à-dire  dans la zone qui nous intéresse actuellement. La force motrice est donc: F = B x L x U/R. Exprimée en fonction de ρ : F = B x L x U x S/(ρ x L).

B. L et S étant constants, si on néglige la dilatation du fil, on obtient: F = K x U/ρ.

La résistivité varie selon la formule suivante :ρ = ρo x (1 + α x δT). ρo et α étant des coefficients propres au matériau et δT la variation de température. La force s'écrit alors: F = K x U / (ρo x (1 + α x δT). Pour le cuivre. ρo  = 1.6.10-4 et α = 4.10-3 (valeurs arrondies).

Application

Variation de la force motrice entre 25° et 200°, limite actuelle supportable par les colles et la dilatation du fil des bobines de HP. F25/F200= 1 + (4. 10-3 X 175) = 1.7. En termes clairs, lorsque la bobine est très chaude, le moteur du HP a perdu plus de 40 % de sa force. La résistance a été multipliée par 1,7 dans la foulée, c'est-à-dire qu'elle est passée d'environ 6.5 ohms (valeur standard de Re pour un HP de 8 ohms) à 11 ohms. Sachant que la puissance max d'un HP est toujours annoncée, c'est la norme, sur sa valeur nominale d'impédance. votre beau HP de 1 000 W sous 8 ohms ne supporte en pratique que 1 000 x 8 / 11 soit environ 700 W.

C'est d'autant mieux pour l'ampli qui, lui, a sa puissance nominale mesurée sur une vraie valeur résistive.

Je vous laisse cogiter et digérer ces quelques informations et je vous donne rendez-vous le mois prochain.

Acoustiquement vôtre.

Alain Pouillon-Guibert Ingénieur-conseil diplômé ESME. Consultant en acoustique et électroacoustique

Partie 3 sur les HP et caissons de basse

PETIT RAPPEL SUR LA STRUCTURE D'UN HP DE GRAVE

Comment fonctionne notre quasi centenaire haut-parleur électrody­namique ? Eh oui. maintes fois cri­tiqué mais toujours utilisé, ce bon vieux HP a gagné ses galons au fils des ans et des améliorations successives qui lui ont été appor­tées. mais sa structure (figure 1) reste inchangée. Un aimant per­manent dont le flux magnétique est concentré sur une bobine de fil conducteur traversée par un cou­rant provenant de l'amplificateur forme le "moteur" du HP. Sur cette bobine est fixée une membrane sensiblement conique dont le dia­mètre extérieur va déterminer la surface de radiation du HP. Le tout étant maintenu et centré par deux suspensions, l'une visible de l'ex­térieur, la suspension périphérique et l'autre, plus discrète mais tout autant indispensable, le spider. Pour obtenir le volume d'air dépla­cé maximum, les constructeurs actuels ont pour cible les grands déplacements de membrane (en restant dans une zone de fonc­tionnement linéaire).

QUELLES SONT LES FACTEURS MÉCANIQUES QUI LIMITENT LE DÉPLACEMENT DE LA MEMBRANE?

Sur les figures 2 et 3. le champ magnétique est représenté (de façon schématique) en bleu. Le déplacement de la bobine est limité par l'obligation de conser­ver une force motrice proportion­nelle au courant qui la traverse (F = B x I x L). B étant constant dans l'entrefer, il faut donc que la lon­gueur de fil L le soit aussi.

Or, si le déplacement est tel qu'une partie de la bobine sort du champ, la force n'est plus proportionnelle au cou­rant. Au repos, la plaque de champ est positionnée au milieu de la bobine et la hauteur de bobinage est toujours supérieure à la hau­teur de la plaque de champ. Le mouvement étant alternatif, il est facile de calculer la valeur limite du déplacement linéaire. Hg est la hauteur de la plaque de champ. Hc est la hauteur de la bobine.

La valeur de déplacement linéaire maxi (théorique) est : Xmax = (Hc - Hg) / 2 Lorsque le déplacement de la bobi­ne dépasse la valeur Xmax (figure 4), il y a donc de la distorsion.

Que se passe-t-il si le vilain DJ qui n'entend pas la disto continue à monter le volume ? Non seulement la distorsion va continuer à aug­menter, mais l'équipage mobile va bientôt se trouver dans une situa­tion critique (figure 5) qui, si elle persiste, va entraîner la casse méca­nique du HP. Si le HP est bien étu­dié. la suspension périphérique va se déformer et atteindre une valeur limite qui va empêcher la bobine de sortir violemment de l'entrefer (figure 6) et de retomber en butant sur le noyau et la plaque de champ, ce qui arrive sur des HP mal étu­diés. A long terme, le HP va non seulement émettre des cris déchi­rants et des craquements lugubres, mais la membrane à laquelle on infli­ge le supplice de l'écartèlement(2) va se déchirer et je vous souhaite bon courage pour faire prendre la répa­ration sous garantie...

WATTS ÉLECTRIQUES ET WATTS ACOUSTIQUES

Le but d'un HP de ce type étant de transformer la puissance élec­trique fournie par l'amplificateur en puissance sonore, atteint-il cor­rectement sa cible ? Un des para­mètres mesurables est le rende­ment du HP exprimé en pourcentage, à ne pas confondre avec l'efficacité (ou sensibilité) exprimée en dB SPL (bien que les deux soient liés). La puissance acoustique Pa est exprimée en watts (W). alors que la capsule du microphone placée dans le champ sonore mesure une intensité sonore (W/m2) généralement exprimée en dB SPL La formule reliant ces deux grandeurs est : I = Pa/S. Dans cette formule I est exprimée en W/m2, Pa en W et S en m2.

Une parenthèse pour rappeler que la pression sonore, ρ, est liée à l'intensité sonore I par I = ρ2/Za où Za est  l'impédance acoustique de l'air.

Et que SPL (en dB) = 20 log ρ/ρo (où ρo représente le niveau de pression de référence, seuil de l'audi-bilité. soit 2.10-5 Pa). Si on part du principe que la puissance est conservée depuis la source jusqu'à la capsule du microphone, on s'aperçoit que l'intensité mesurée décroit inversement proportionnellement avec l'augmentation de la surface, généralement sphérique centrée sur la source. C'est-à-dire, de façon inversement proportionnelle au carré du rayon, donc de la distance à la source. Pour faire simple, la puissance sonore générée par la source va ensuite 's'étaler* dans toutes les directions et on ne pourra donc mesurer que l'intensité en chaque point de l'espace.

ORDRE D'IDÉE DES RENDEMENTS DES HP DE GRAVE

Le calcul du rendement d'un HP est le suivant :

n0 = (4Pi2 x Fs3 x Vas)/(c3 x Qes) Fs étant la fréquence de résonance du HP à l'air libre. Vas le volume d'air équivalent (élasticité pneumatique) au HP (3), c la vitesse de transmission du son dans l'air et Qes le facteur de qualité électrique du HP.

Application

Calcul du rendement d'un excellent HP de 38 cm destiné à l'extrême-grave, limite vers 25 Hz.

Fs = 28 Hz, Vas = 0.2 m3, Qes = 0.27, no= 1.5%.

Dans la même série, mais destiné au grave seulement, limite vers 45 Hz.

Fs = 40 Hz. Vas = 0,18 m3. Qes = 0,25. no = 4,5 %.

Intéressant non ? Pour 500 W électriques, le premier fournira 7.5 W acoustiques, alors que le second sera capable de trois fois plus, soit 22,5 W acoustiques. Pour générer du grave, il faut non seulement être capable de faire bouger de l'air, mais encore doit-on pouvoir transformer l'énergie fournie par l'ampli en son et non en chaleur. Car les 95,5 % d'énergie transformée le sont par effet joule, principe de fonctionnement d'un fer à repasser. Non seulement un HP n'est pas un ustensile franchement adapté au repassage (de luxe), mais encore la chaleur dégagée va poser des problèmes qui vont commencer par un effet de compression thermique et finiront par aboutir, si on insiste. au service de SAV de votre fournisseur.

(1) Pourquoi le diamètre émissif réel du HP est-il inférieur à son dia­mètre nominal? Là encore, un petit dessin explicatif (figure 7): Un HP de grave fonctionne comme un piston, le déplace­ment de la bobine est intégrale­ment transmis à la membrane. La suspension périphérique de la membrane sert donc de liai­son mécanique entre l'extérieur du cône et le saladier. Seule la portion de suspension fixée sur la membrane suit parfaitement le mouvement, la partie fixée sur le saladier ne bouge pas. Le milieu de la suspension a donc un dépla­cement. dans la zone de fonc­tionnement linéaire, sensible­ment égal à la moitié du déplacement du cône. C'est ce diamètre qui doit être considéré comme diamètre 'actif du HP.

Application :

Considérons un HP d'origine PHL Audio de 38 cm. Sa surface émissive donnée par le constructeur est Sd = 0.0892 m2 Ce qui correspond à un diamètre actif de 33.7 cm. Le diamètre extérieur du HP étant de 37.5 cm. on peut calculer le rapport entre ces deux diamètres :

Dactif/Dext = 33.7/37.5 = 90%. Le constructeur a optimisé le remplissage de son HP. sachant que ce sont les quelques mm gagnés sur le diamètre émissif qui font gagner de la surface. S = Pi x D2/4.. Plus on arrive à 'gratter' sur le diamètre émissif. plus le gain de surface active est important. Considérons maintenant un HP d'origine Xxx de 38 cm. Surface émissive Sd = 0.083 m3. Donc, diamètre actif = 32.5 cm. Diamètre extérieur = 38.8 m. Rapport Dactif/Dext = 32,5/38.8 = 84 %. Le remplissage est nettement moins favorable. Si je compare ces deux HP et calcule le rapport des surfaces émissives. S1 /S2 = 0.0892/0.0830 = 1.08. Il faudra donc augmenter le déplacement du second de 8 % pour obtenir le même volume d'air, et pourtant, son diamètre extérieur est supérieur au premier. On pourrait aller plus loin et comparer les valeurs de Xmax. déplacement linéaire maxi de la membrane, les rendements et les autres paramètres. mais mon propos actuel n'est pas de traiter de l'ingénierie des HP de grave, j'en resterai donc là. Tout ceci pour pointer du doigt les problèmes auxquels sont confrontés les concepteurs d'encemtes. tout au moins ceux qui savent de quoi ils parlent mais ceci est une autre histoire. ...

(2) L'écartèlement était un supplice utilisé pour donner la mort par la séparation simultanée des quatre membres du tronc du corps. Il servait également dans le cadre de la torture judiciaire.

(3) A la fin des années 60. deux physiciens australiens. Neville Thiele et Richard Small, appliquèrent les méthodes de calcul (de synthèse) des filtres analogiques au fonctionnement des HP électrodynamiques et décrivirent les paramètres qui por­tent leurs noms et sont encore uti­lisés de nos jours pour calculer et simuler le fonctionnement des HP dans le grave.

Jusqu'à cette époque, un grand flou artistique régnait en maître sur la conception des enceintes dans le grave, et on utilisait des méthodes empiriques. Chacun avait sa propre recette et son fee­ling pour sentir le vent “au doigt mouillé”.

C'est grâce à Thiele et Small que la conception des enceintes dans le grave est passée du domaine de la recette de cuisine (disons largement empirique) à celui du calcul mathé­matique.

LES PARAMÈTRES DE THIELE ET SMALL

Re : Résistance de la bobine mobile. Cette valeur est toujours inférieure à l'impédance nominale du HP car elle correspond â la résistance du fil de bobinage mesurée en courant continu et non pas à l'impédance dans laquelle vient s'ajouter l'impédance propre de l'inductance formée par la bobine et les autres propriétés mécaniques du HP.

Fs : Fréquence de résonance du HP à l'air libre.

Mms : Masse mécanique totale des parties en mouvement, incluant la masse d'air mise en mouvement. Mms est mesurée à l'air libre.

Qes: Facteur de qualité électrique Valeur descriptive de la résonance électrique du HP à Fs. Plus la valeur de Qes est faible, plus grand est l'amortissement de la résonance.

Qms : Facteur de qualité mécanique. Idem que Qes mais pour les valeurs mécaniques Cette valeur est importante dans le choix d'un HP de grave, plus elle est élevée, plus le HP se rapproche d'un ressort idéal sans amortissement.

Qts : Facteur de qualité total Correspond à la mise en parallèle de Qms et Qes. 1/Qts = 1/Qms + 1/Qes. Soit Qts = (Qms x Qts) / (Qms + Qts)

C'est Qts qui entre dans le calcul de la fréquence d'accord d'un bass-reflex

Cms: Compliance ou élasticité mécanique, inverse de la raideur pour un ressort

BL : Produit de l'induction magnétique dans l'entrefer par la longueur de fil baignée d3ns le champ magnétique, ou facteur de force. Sachant que la force qui meut la bobine est égale à F = B x I x L. I étant la valeur du courant qui traverse la bobine, plus le BL est élevé, plus la force motrice l'est aussi.

Le : Inductance (électrique) de la bobine mobile. Cette valeur n'est pas constante avec la fréquence.

Sd: Surface de rayonnement de la membrane

Vas: Volume d'air équivalent à Cms. En effet, un volume d'air clos forme un ressort. Cette propriété est aussi utilisée en automobile dans les suspensions pneumatiques Vas = ρ  x c2 x Sd2 x Cms.

ρ est la densité de l'air (masse volumique) à ne pas confondre avec la résistivité vue plus haut (c'est la même notation), c la vitesse du son dans l'air. Les valeurs généralement utilisées sont les suivantes c = 344 m/s, ρ = 1,2 kg/m3 (au niveau de la mer à 20 °C).

Soit Vas - 142000 x Sd2 x Cms.

Un sub JBL SRX728S. Deux 18" en bass-reflex. 136 dB SPL crête.

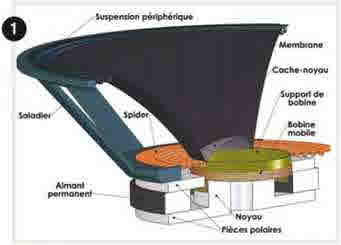
FIGURE 01 / Structure d'un haut-parleur de grave.

FIGURE 02 / Bobine mobile au repos

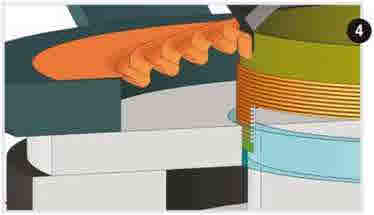
FIGURE 04 / Déplacement supérieur à Xmax (limite d’excursion linéaire)

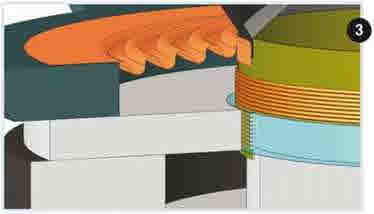
FIGURE 03 / Limite de déplacement (excursion) linéaire.

FIGURE 05 / Déplacement limit Xdam (damage : détérioration).

FIGURE 6 / Ce déplacement (excursion) extrême risque de conduire à la destruction irréversible.

Figure 7 : Explication du diamètre émissif de la membrane (ou de la surface d’émission SD).

Neville Thiele (a gauche) et Richard Small.